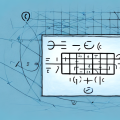
The greatest common factor (GCF) of two numbers is the largest number that evenly divides both numbers. For example, if you are asked to find the greatest common factor of 8 and 20, the answer is 4. In this article, we will explain different ways of calculating the GCF of 8 and 20, as well as understanding and utilizing the GCF of numbers in general.
How to Calculate the Greatest Common Factor of 8 and 20
The easiest way to calculate the GCF of a pair of numbers is by utilizing what is known as prime factorization. This is a method in which both numbers are broken down into their prime factors – that is, their smallest factors that are only divisible by themselves and one – and then finding the largest common factor among them. In the case of 8 and 20, the prime factors of 8 are 2 x 2 x 2, and the prime factors of 20 are 2 x 2 x 5. Therefore, the greatest common factor (the largest number that both are divisible by) is 2 x 2, or 4.
Once the GCF is determined, it can be used to simplify fractions or to solve other mathematical problems. For example, if you wanted to simplify the fraction 8/20, you would divide both the numerator and denominator by the GCF of 4, resulting in the simplified fraction 2/5.
Understanding the Greatest Common Factor
The greatest common factor, or GCF, can tell us a lot about the relationship between two numbers. In mathematics, it is used for all sorts of situations – from calculating ratios to dividing fractions. Understanding the GCF of two numbers can also tell us how likely it is for them to share common factors. For example, a GCF of 4 between 8 and 20 means that there is a very high chance of them having more than one factor in common.
Finding the Greatest Common Factor Using Prime Factorization
The prime factors of a number are those that cannot be divided further without going into decimals or fractions. To find the greatest common factor (GCF) using prime factorization, you must break down each number into its prime factors, then find the largest number that can be created from the common prime factors among them. To find the prime factors of 8 and 20, we use the following steps:
- 8: 2 x 2 x 2
- 20: 2 x 2 x 5
As we can see, both 8 and 20 have two factors in common: 2 x 2. Therefore, the greatest common factor of 8 and 20 is 4.
Examples of How to Find the Greatest Common Factor of 8 and 20
Now that we understand how to calculate the greatest common factor (GCF) using prime factorization, let’s look at some examples. Here are some example calculations for finding the GCF of 8 and 20:
- GCF of 8 and 20: 2 x 2 = 4
- GCF of 16 and 12: 2 x 2 x 3 = 12
- GCF of 9 and 18: 3 x 3 = 9
As we can see from these examples, knowing how to calculate the greatest common factor (GCF) using prime factorization can come in handy in many situations.
Using the Euclidean Algorithm to Find the Greatest Common Factor
The Euclidean Algorithm is another useful tool for finding the greatest common factor (GCF) of two numbers. This approach involves counting up from the larger number until a common factor is found. The advantage of this method is that it can be used to find a GCF of more than two numbers at once. Here’s an example showing how it works to find the greatest common factor of 8 and 20.
- Start with 8
- Count up by 8 until you get to 20 (8 + 8 = 16; 16 + 4 = 20)
- The “counting up” number is our GCF (4)
The Euclidean Algorithm gives us a quick and easy way to calculate the GCF of two or more numbers at once, which can come in very handy in certain situations.
Advantages of Knowing the Greatest Common Factor of 8 and 20
Knowing the greatest common factor of two numbers can be incredibly useful for solving complex mathematical problems. For example, if you are trying to divide a large number by 8 and 20, you can use their GCF (4) to reduce the number by one-fourth instead. This reduces the problem from a difficult one to a much simpler version with one less step.
Benefits of Understanding the Greatest Common Factor
In addition to being incredibly useful for solving mathematical problems, understanding what the greatest common factor (GCF) is can also help us develop our analytical thinking skills. By recognizing patterns in factors among different pairs of numbers, we can learn how data relates to each other and make more accurate predictions.
We hope this article has provided you with a basic understanding of what the greatest common factor is and how to calculate it. Knowing this concept will open up a world of possibilities when it comes to solving mathematical problems, so make sure to spend some time honing your skills!